

#Golden rectangle ratio full
The DNA molecule measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral. You can also take this idea and create a golden rectangle. This formula can help you when creating shapes, logos, layouts, and more. DNA moleculesĮven the microscopic realm is not immune to Fibonacci. You can find the Golden Ratio when you divide a line into two parts and the longer part (a) divided by the smaller part (b) is equal to the sum of (a) + (b) divided by (a), which both equal 1.618. When a hawk approaches its prey, its sharpest view is at an angle to their direction of flight - an angle that's the same as the spiral's pitch. And as noted, bee physiology also follows along the Golden Curve rather nicely. For example, the 50th Fibonacci number is 20365011074.
#Golden rectangle ratio series
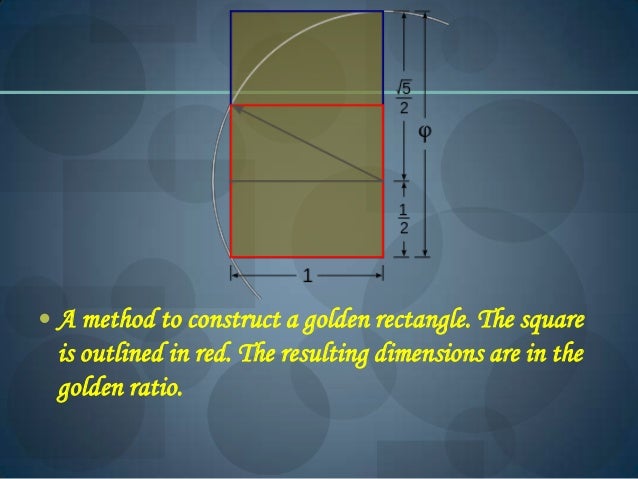
These rectangles are called golden rectangles. The ratio of one Fibonacci number to the previous in the series gets closer and closer to the Golden Ratio as you get to higher and higher Fibonacci numbers. If a is the width and a + b the length of the rectangle, then the golden ratio is. Greek sculptor and mathematician Phidias applied phi to the design of the Parthenon, built in 440 BC, which features structural columns that form golden rectangles. Recall that a ratio is the relationship between two quantities, represented generally as a fraction. The discovery of the golden ratio can be attributed to many different thinkers throughout history. Following the same pattern, females have 2, 3, 5, 8, 13, and so on. Hence, the new rectangle in blue has the same ratio of the large side to the small side as the original one. Seen throughout architecture and nature, the golden rectangle is a rectangle whose sides are in what is called the golden ratio. Golden rectangles exhibit a special form of self-similarity: All rectangles created by adding or removing a square from an end are golden rectangles as well. Results of phase 3 (drawn rectangles) Participants that drew a golden. In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio,, which is (the Greek letter phi), where is approximately 1.618. The ratio of the length to the width of the large rectangle equals the ratio of length to width of the smaller rectangle.

This article discusses how knowledge about golden ratio can be used in jewelry design. was fulfilled (where r is the sides’ ratio), the rectangle was considered a golden. Thus, when it comes to the family tree, males have 2, 3, 5, and 8 grandparents, great-grandparents, gr-gr-grandparents, and gr-gr-gr-grandparents respectively. First Online: 07 July 2018 342 Accesses Part of the Advances in Intelligent Systems and Computing book series (AISC,volume 809) Abstract The golden ratio has universal application and provides maximum performance in an artistic composition. Males have one parent (a female), whereas females have two (a female and male). The ratio is derived from an ancient Indian mathematical formula.

In addition, the family tree of honey bees also follows the familiar pattern. The golden ratio is an irrational number that is equal to (1+5)/2, or approximately 1.618. The answer is typically something very close to 1.618. The most profound example is by dividing the number of females in a colony by the number of males (females always outnumber males). Columbia University.Speaking of honey bees, they follow Fibonacci in other interesting ways. “Private tutoring and its impact on students' academic achievement, formal schooling, and educational inequality in Korea.” Unpublished doctoral thesis. If the ratio of arcs a/b, then angle subtended by the.
#Golden rectangle ratio professional
Tutors, instructors, experts, educators, and other professionals on the platform are independent contractors, who use their own styles, methods, and materials and create their own lesson plans based upon their experience, professional judgment, and the learners with whom they engage. In this website the golden ratio is denoted by the Greek lowercase letter phi (): 1.6180339887, while its inverse, (1/phi), which is also equal to (phi-1). A golden triangle is an isosceles triangle where the ratio of the longer side to the base is.
Varsity Tutors connects learners with a variety of experts and professionals. Varsity Tutors does not have affiliation with universities mentioned on its website. Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors.Īward-Winning claim based on CBS Local and Houston Press awards. Names of standardized tests are owned by the trademark holders and are not affiliated with Varsity Tutors LLC.Ĥ.9/5.0 Satisfaction Rating based upon cumulative historical session ratings through 12/31/20.


 0 kommentar(er)
0 kommentar(er)
